Deep Learning & Art: Neural Style Transfer

In this assignment, you will learn about Neural Style Transfer. This algorithm was created by Gatys et al. (2015).

In this assignment, you will:

• Implement the neural style transfer algorithm
• Generate novel artistic images using your algorithm

Most of the algorithms you've studied optimize a cost function to get a set of parameter values. In Neural Style Transfer, you'll optimize a cost function to get pixel values!

Updates

If you were working on the notebook before this update...

• The current notebook is version "3a".
• You can find your original work saved in the notebook with the previous version name ("v2")
• To view the file directory, go to the menu "File->Open", and this will open a new tab that shows the file directory.

List of updates

• Use pprint.PrettyPrinter to format printing of the vgg model.
• computing content cost: clarified and reformatted instructions, fixed broken links, added additional hints for unrolling.
• style matrix: clarify two uses of variable "G" by using different notation for gram matrix.
• style cost: use distinct notation for gram matrix, added additional hints.
• Grammar and wording updates for clarity.
• model_nn: added hints.

import os
import sys
import scipy.io
import scipy.misc
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow
from PIL import Image
from nst_utils import *
import numpy as np
import tensorflow as tf
import pprint
%matplotlib inline

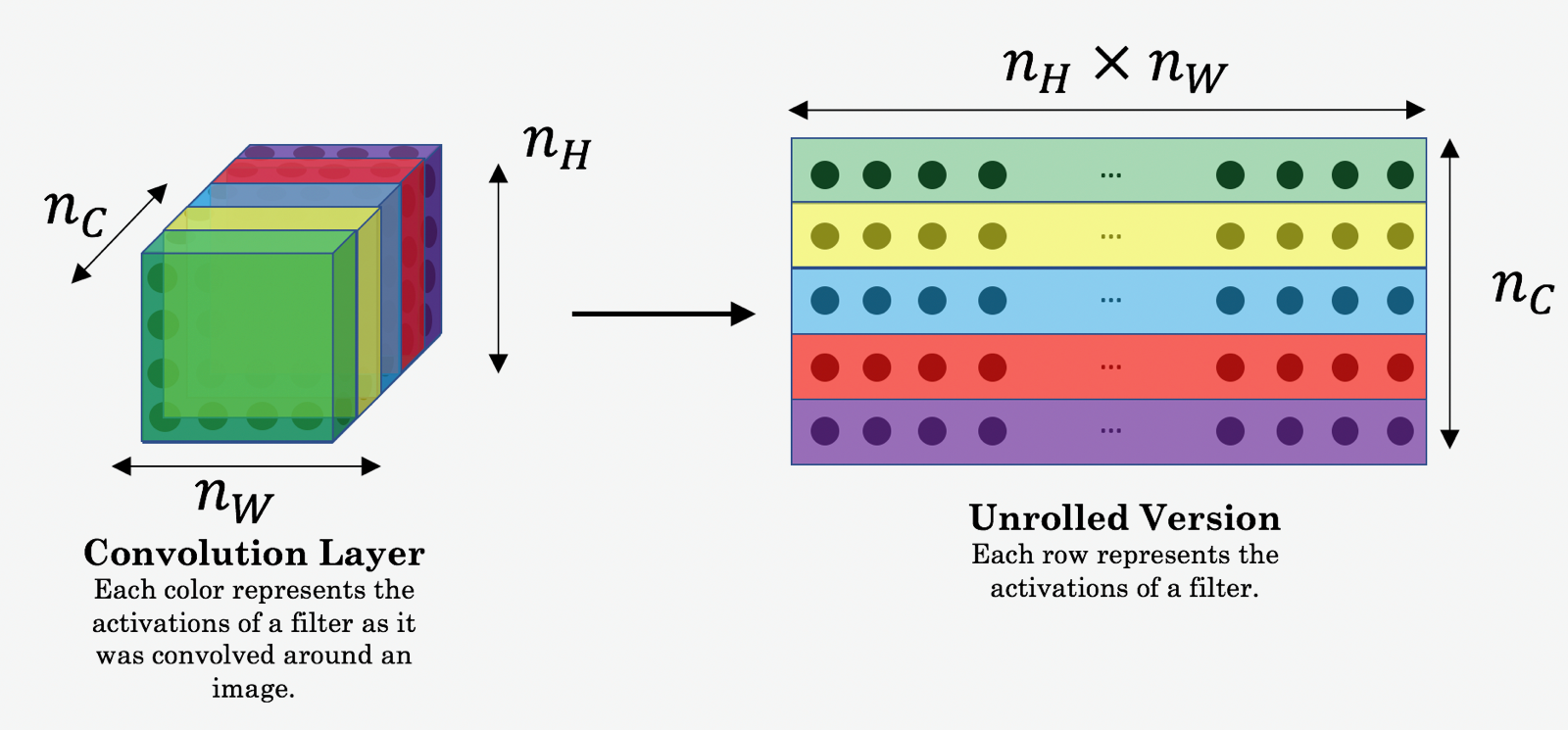
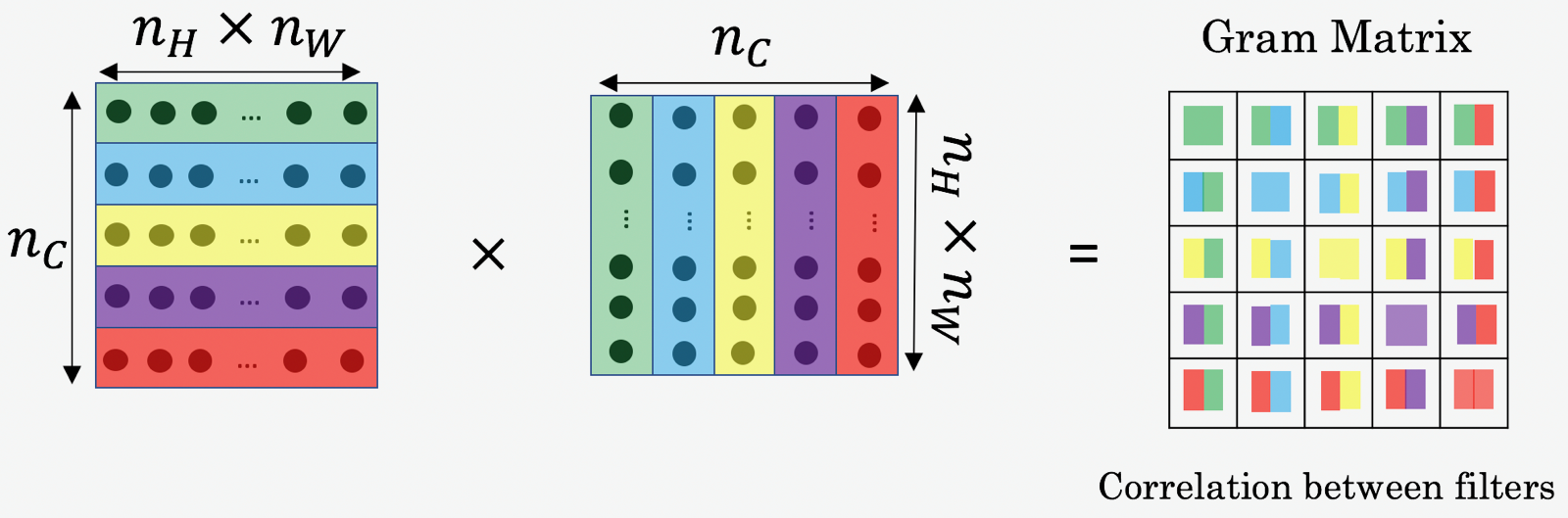
1 - Problem Statement

Neural Style Transfer (NST) is one of the most fun techniques in deep learning. As seen below, it merges two images, namely: a "content" image (C) and a "style" image (S), to create a "generated" image (G).

The generated image G combines the "content" of the image C with the "style" of image S.

In this example, you are going to generate an image of the Louvre museum in Paris (content image C), mixed with a painting by Claude Monet, a leader of the impressionist movement (style image S).

Let's see how you can do this.

2 - Transfer Learning

Neural Style Transfer (NST) uses a previously trained convolutional network, and builds on top of that. The idea of using a network trained on a different task and applying it to a new task is called transfer learning.

Following the original NST paper, we will use the VGG network. Specifically, we'll use VGG-19, a 19-layer version of the VGG network. This model has already been trained on the very large ImageNet database, and thus has learned to recognize a variety of low level features (at the shallower layers) and high level features (at the deeper layers).

Run the following code to load parameters from the VGG model. This may take a few seconds.

pp = pprint.PrettyPrinter(indent=4)
model = load_vgg_model("pretrained-model/imagenet-vgg-verydeep-19.mat")
pp.pprint(model)

{   'avgpool1': <tf.Tensor 'AvgPool:0' shape=(1, 150, 200, 64) dtype=float32>,
    'avgpool2': <tf.Tensor 'AvgPool_1:0' shape=(1, 75, 100, 128) dtype=float32>,
    'avgpool3': <tf.Tensor 'AvgPool_2:0' shape=(1, 38, 50, 256) dtype=float32>,
    'avgpool4': <tf.Tensor 'AvgPool_3:0' shape=(1, 19, 25, 512) dtype=float32>,
    'avgpool5': <tf.Tensor 'AvgPool_4:0' shape=(1, 10, 13, 512) dtype=float32>,
    'conv1_1': <tf.Tensor 'Relu:0' shape=(1, 300, 400, 64) dtype=float32>,
    'conv1_2': <tf.Tensor 'Relu_1:0' shape=(1, 300, 400, 64) dtype=float32>,
    'conv2_1': <tf.Tensor 'Relu_2:0' shape=(1, 150, 200, 128) dtype=float32>,
    'conv2_2': <tf.Tensor 'Relu_3:0' shape=(1, 150, 200, 128) dtype=float32>,
    'conv3_1': <tf.Tensor 'Relu_4:0' shape=(1, 75, 100, 256) dtype=float32>,
    'conv3_2': <tf.Tensor 'Relu_5:0' shape=(1, 75, 100, 256) dtype=float32>,
    'conv3_3': <tf.Tensor 'Relu_6:0' shape=(1, 75, 100, 256) dtype=float32>,
    'conv3_4': <tf.Tensor 'Relu_7:0' shape=(1, 75, 100, 256) dtype=float32>,
    'conv4_1': <tf.Tensor 'Relu_8:0' shape=(1, 38, 50, 512) dtype=float32>,
    'conv4_2': <tf.Tensor 'Relu_9:0' shape=(1, 38, 50, 512) dtype=float32>,
    'conv4_3': <tf.Tensor 'Relu_10:0' shape=(1, 38, 50, 512) dtype=float32>,
    'conv4_4': <tf.Tensor 'Relu_11:0' shape=(1, 38, 50, 512) dtype=float32>,
    'conv5_1': <tf.Tensor 'Relu_12:0' shape=(1, 19, 25, 512) dtype=float32>,
    'conv5_2': <tf.Tensor 'Relu_13:0' shape=(1, 19, 25, 512) dtype=float32>,
    'conv5_3': <tf.Tensor 'Relu_14:0' shape=(1, 19, 25, 512) dtype=float32>,
    'conv5_4': <tf.Tensor 'Relu_15:0' shape=(1, 19, 25, 512) dtype=float32>,
    'input': <tf.Variable 'Variable:0' shape=(1, 300, 400, 3) dtype=float32_ref>}

• The model is stored in a python dictionary.
• The python dictionary contains key-value pairs for each layer.
• The 'key' is the variable name and the 'value' is a tensor for that layer.

Assign input image to the model's input layer

To run an image through this network, you just have to feed the image to the model. In TensorFlow, you can do so using the tf.assign function. In particular, you will use the assign function like this:

model["input"].assign(image)

This assigns the image as an input to the model.

Activate a layer

After this, if you want to access the activations of a particular layer, say layer 4_2 when the network is run on this image, you would run a TensorFlow session on the correct tensor conv4_2, as follows:

sess.run(model["conv4_2"])

3 - Neural Style Transfer (NST)

We will build the Neural Style Transfer (NST) algorithm in three steps:

• Build the content cost function $J_{content}(C,G)$
• Build the style cost function $J_{style}(S,G)$
• Put it together to get $J(G) = \alpha J_{content}(C,G) + \beta J_{style}(S,G)$.

3.1 - Computing the content cost

In our running example, the content image C will be the picture of the Louvre Museum in Paris. Run the code below to see a picture of the Louvre.

content_image = scipy.misc.imread("images/louvre.jpg")
imshow(content_image);

The content image (C) shows the Louvre museum's pyramid surrounded by old Paris buildings, against a sunny sky with a few clouds.

3.1.1 - Make generated image G match the content of image C

Shallower versus deeper layers

• The shallower layers of a ConvNet tend to detect lower-level features such as edges and simple textures.
• The deeper layers tend to detect higher-level features such as more complex textures as well as object classes.

Choose a "middle" activation layer $a^{[l]}$

We would like the "generated" image G to have similar content as the input image C. Suppose you have chosen some layer's activations to represent the content of an image.

• In practice, you'll get the most visually pleasing results if you choose a layer in the middle of the network--neither too shallow nor too deep.
• (After you have finished this exercise, feel free to come back and experiment with using different layers, to see how the results vary.)

Forward propagate image "C"

• Set the image C as the input to the pretrained VGG network, and run forward propagation.
• Let $a^{(C)}$ be the hidden layer activations in the layer you had chosen. (In lecture, we had written this as $a^{[l](C)}$, but here we'll drop the superscript $[l]$ to simplify the notation.) This will be an $n_H \times n_W \times n_C$ tensor.

Forward propagate image "G"

• Repeat this process with the image G: Set G as the input, and run forward progation.
• Let $a^{(G)}$ be the corresponding hidden layer activation.

Content Cost Function $J_{content}(C,G)$

We will define the content cost function as:

$$J_{content}(C,G) = \frac{1}{4 \times n_H \times n_W \times n_C}\sum _{ \text{all entries}} (a^{(C)} - a^{(G)})^2\tag{1} $$

• Here, $n_H, n_W$ and $n_C$ are the height, width and number of channels of the hidden layer you have chosen, and appear in a normalization term in the cost.
• For clarity, note that $a^{(C)}$ and $a^{(G)}$ are the 3D volumes corresponding to a hidden layer's activations.
• In order to compute the cost $J_{content}(C,G)$, it might also be convenient to unroll these 3D volumes into a 2D matrix, as shown below.
• Technically this unrolling step isn't needed to compute $J_{content}$, but it will be good practice for when you do need to carry out a similar operation later for computing the style cost $J_{style}$.

Exercise: Compute the "content cost" using TensorFlow.

Instructions: The 3 steps to implement this function are:

1. Retrieve dimensions from a_G:
   • To retrieve dimensions from a tensor X, use: X.get_shape().as_list()
2. Unroll a_C and a_G as explained in the picture above
   • You'll likey want to use these functions: tf.transpose and tf.reshape.
3. Compute the content cost:
   • You'll likely want to use these functions: tf.reduce_sum, tf.square and tf.subtract.

Additional Hints for "Unrolling"

• To unroll the tensor, we want the shape to change from $(m,n_H,n_W,n_C)$ to $(m, n_H \times n_W, n_C)$.
• tf.reshape(tensor, shape) takes a list of integers that represent the desired output shape.
• For the shape parameter, a -1 tells the function to choose the correct dimension size so that the output tensor still contains all the values of the original tensor.
• So tf.reshape(a_C, shape=[m, n_H * n_W, n_C]) gives the same result as tf.reshape(a_C, shape=[m, -1, n_C]).
• If you prefer to re-order the dimensions, you can use tf.transpose(tensor, perm), where perm is a list of integers containing the original index of the dimensions.
• For example, tf.transpose(a_C, perm=[0,3,1,2]) changes the dimensions from $(m, n_H, n_W, n_C)$ to $(m, n_C, n_H, n_W)$.
• There is more than one way to unroll the tensors.
• Notice that it's not necessary to use tf.transpose to 'unroll' the tensors in this case but this is a useful function to practice and understand for other situations that you'll encounter.

# GRADED FUNCTION: compute_content_cost

def compute_content_cost(a_C, a_G):
    """
    Computes the content cost
    
    Arguments:
    a_C -- tensor of dimension (1, n_H, n_W, n_C), hidden layer activations representing content of the image C 
    a_G -- tensor of dimension (1, n_H, n_W, n_C), hidden layer activations representing content of the image G
    
    Returns: 
    J_content -- scalar that you compute using equation 1 above.
    """
    
    ### START CODE HERE ###
    # Retrieve dimensions from a_G (≈1 line)
    m, n_H, n_W, n_C = a_G.get_shape().as_list()
    
    # Reshape a_C and a_G (≈2 lines)
    a_C_unrolled = tf.reshape(a_C, shape=[m, n_H*n_W, n_C])
    a_G_unrolled = tf.reshape(a_G, shape=[m, n_H*n_W, n_C])
    
    # compute the cost with tensorflow (≈1 line)
    J_content = (1/(4*n_H*n_W*n_C))*(tf.reduce_sum(tf.square(tf.subtract(a_C_unrolled,a_G_unrolled))))
    ### END CODE HERE ###
    
    return J_content

tf.reset_default_graph()

with tf.Session() as test:
    tf.set_random_seed(1)
    a_C = tf.random_normal([1, 4, 4, 3], mean=1, stddev=4)
    a_G = tf.random_normal([1, 4, 4, 3], mean=1, stddev=4)
    J_content = compute_content_cost(a_C, a_G)
    print("J_content = " + str(J_content.eval()))

J_content = 6.76559

Expected Output:

**J_content**

6.76559

What you should remember

• The content cost takes a hidden layer activation of the neural network, and measures how different $a^{(C)}$ and $a^{(G)}$ are.
• When we minimize the content cost later, this will help make sure $G$ has similar content as $C$.

3.2 - Computing the style cost

For our running example, we will use the following style image:

style_image = scipy.misc.imread("images/monet_800600.jpg")
imshow(style_image);

This was painted in the style of impressionism.

Lets see how you can now define a "style" cost function $J_{style}(S,G)$.

3.2.1 - Style matrix

Gram matrix

• The style matrix is also called a "Gram matrix."
• In linear algebra, the Gram matrix G of a set of vectors $(v_{1},\dots ,v_{n})$ is the matrix of dot products, whose entries are ${\displaystyle G_{ij} = v_{i}^T v_{j} = np.dot(v_{i}, v_{j}) }$.
• In other words, $G_{ij}$ compares how similar $v_i$ is to $v_j$: If they are highly similar, you would expect them to have a large dot product, and thus for $G_{ij}$ to be large.

Two meanings of the variable $G$

• Note that there is an unfortunate collision in the variable names used here. We are following common terminology used in the literature.
• $G$ is used to denote the Style matrix (or Gram matrix)
• $G$ also denotes the generated image.
• For this assignment, we will use $G_{gram}$ to refer to the Gram matrix, and $G$ to denote the generated image.

Compute $G_{gram}$

In Neural Style Transfer (NST), you can compute the Style matrix by multiplying the "unrolled" filter matrix with its transpose:

$$\mathbf{G}_{gram} = \mathbf{A}_{unrolled} \mathbf{A}_{unrolled}^T$$

$G_{(gram)i,j}$: correlation

The result is a matrix of dimension $(n_C,n_C)$ where $n_C$ is the number of filters (channels). The value $G_{(gram)i,j}$ measures how similar the activations of filter $i$ are to the activations of filter $j$.

$G_{(gram),i,i}$: prevalence of patterns or textures

• The diagonal elements $G_{(gram)ii}$ measure how "active" a filter $i$ is.
• For example, suppose filter $i$ is detecting vertical textures in the image. Then $G_{(gram)ii}$ measures how common vertical textures are in the image as a whole.
• If $G_{(gram)ii}$ is large, this means that the image has a lot of vertical texture.

By capturing the prevalence of different types of features ($G_{(gram)ii}$), as well as how much different features occur together ($G_{(gram)ij}$), the Style matrix $G_{gram}$ measures the style of an image.

Exercise:

• Using TensorFlow, implement a function that computes the Gram matrix of a matrix A.
• The formula is: The gram matrix of A is $G_A = AA^T$.
• You may use these functions: matmul and transpose.

# GRADED FUNCTION: gram_matrix

def gram_matrix(A):
    """
    Argument:
    A -- matrix of shape (n_C, n_H*n_W)
    
    Returns:
    GA -- Gram matrix of A, of shape (n_C, n_C)
    """
    
    ### START CODE HERE ### (≈1 line)
    GA = tf.matmul(A,tf.transpose(A))
    ### END CODE HERE ###
    
    return GA

tf.reset_default_graph()

with tf.Session() as test:
    tf.set_random_seed(1)
    A = tf.random_normal([3, 2*1], mean=1, stddev=4)
    GA = gram_matrix(A)
    
    print("GA = \n" + str(GA.eval()))

GA = 
[[  6.42230511  -4.42912197  -2.09668207]
 [ -4.42912197  19.46583748  19.56387138]
 [ -2.09668207  19.56387138  20.6864624 ]]

Expected Output:

**GA**

[[ 6.42230511 -4.42912197 -2.09668207] [ -4.42912197 19.46583748 19.56387138] [ -2.09668207 19.56387138 20.6864624 ]]

3.2.2 - Style cost

Your goal will be to minimize the distance between the Gram matrix of the "style" image S and the gram matrix of the "generated" image G.

• For now, we are using only a single hidden layer $a^{[l]}$.
• The corresponding style cost for this layer is defined as:

$$J_{style}^{[l]}(S,G) = \frac{1}{4 \times {n_C}^2 \times (n_H \times n_W)^2} \sum _{i=1}^{n_C}\sum_{j=1}^{n_C}(G^{(S)}_{(gram)i,j} - G^{(G)}_{(gram)i,j})^2\tag{2} $$

• $G_{gram}^{(S)}$ Gram matrix of the "style" image.
• $G_{gram}^{(G)}$ Gram matrix of the "generated" image.
• Remember, this cost is computed using the hidden layer activations for a particular hidden layer in the network $a^{[l]}$

Exercise: Compute the style cost for a single layer.

Instructions: The 3 steps to implement this function are:

1. Retrieve dimensions from the hidden layer activations a_G:
   • To retrieve dimensions from a tensor X, use: X.get_shape().as_list()
2. Unroll the hidden layer activations a_S and a_G into 2D matrices, as explained in the picture above (see the images in the sections "computing the content cost" and "style matrix").
   • You may use tf.transpose and tf.reshape.
3. Compute the Style matrix of the images S and G. (Use the function you had previously written.)
4. Compute the Style cost:
   • You may find tf.reduce_sum, tf.square and tf.subtract useful.

Additional Hints

• Since the activation dimensions are $(m, n_H, n_W, n_C)$ whereas the desired unrolled matrix shape is $(n_C, n_H*n_W)$, the order of the filter dimension $n_C$ is changed. So tf.transpose can be used to change the order of the filter dimension.
• for the product $\mathbf{G}_{gram} = \mathbf{A}_{} \mathbf{A}_{}^T$, you will also need to specify the perm parameter for the tf.transpose function.

# GRADED FUNCTION: compute_layer_style_cost

def compute_layer_style_cost(a_S, a_G):
    """
    Arguments:
    a_S -- tensor of dimension (1, n_H, n_W, n_C), hidden layer activations representing style of the image S 
    a_G -- tensor of dimension (1, n_H, n_W, n_C), hidden layer activations representing style of the image G
    
    Returns: 
    J_style_layer -- tensor representing a scalar value, style cost defined above by equation (2)
    """
    
    ### START CODE HERE ###
    # Retrieve dimensions from a_G (≈1 line)
    m, n_H, n_W, n_C = a_G.get_shape().as_list()
    
    # Reshape the images to have them of shape (n_C, n_H*n_W) (≈2 lines)
    a_S = tf.reshape(a_S, shape=[n_H*n_W, n_C])
    a_G = tf.reshape(a_G, shape=[n_H*n_W, n_C])
    #kkp - oder moto shape dile somossa kore, tai shape k ulta kore then traspose kore gram_matrix e pathano hoise. 

    # Computing gram_matrices for both images S and G (≈2 lines)
    GS = gram_matrix(tf.transpose(a_S))
    GG = gram_matrix(tf.transpose(a_G))

    # Computing the loss (≈1 line)
    J_style_layer = 1/(4*(n_C**2)*(n_H*n_W)**2) * (tf.reduce_sum(tf.square(tf.subtract(GS,GG))))
    
    ### END CODE HERE ###
    
    return J_style_layer

tf.reset_default_graph()

with tf.Session() as test:
    tf.set_random_seed(1)
    a_S = tf.random_normal([1, 4, 4, 3], mean=1, stddev=4)
    a_G = tf.random_normal([1, 4, 4, 3], mean=1, stddev=4)
    J_style_layer = compute_layer_style_cost(a_S, a_G)
    
    print("J_style_layer = " + str(J_style_layer.eval()))

J_style_layer = 9.19028

Expected Output:

**J_style_layer**

9.19028

3.2.3 Style Weights

• So far you have captured the style from only one layer.
• We'll get better results if we "merge" style costs from several different layers.
• Each layer will be given weights ($\lambda^{[l]}$) that reflect how much each layer will contribute to the style.
• After completing this exercise, feel free to come back and experiment with different weights to see how it changes the generated image $G$.
• By default, we'll give each layer equal weight, and the weights add up to 1. ($\sum_{l}^L\lambda^{[l]} = 1$)

STYLE_LAYERS = [
    ('conv1_1', 0.2),
    ('conv2_1', 0.2),
    ('conv3_1', 0.2),
    ('conv4_1', 0.2),
    ('conv5_1', 0.2)]

You can combine the style costs for different layers as follows:

$$J_{style}(S,G) = \sum_{l} \lambda^{[l]} J^{[l]}_{style}(S,G)$$

where the values for $\lambda^{[l]}$ are given in STYLE_LAYERS.

Exercise: compute style cost

• We've implemented a compute_style_cost(...) function.
• It calls your compute_layer_style_cost(...) several times, and weights their results using the values in STYLE_LAYERS.
• Please read over it to make sure you understand what it's doing.

Description of compute_style_cost

For each layer:

• Select the activation (the output tensor) of the current layer.
• Get the style of the style image "S" from the current layer.
• Get the style of the generated image "G" from the current layer.
• Compute the "style cost" for the current layer
• Add the weighted style cost to the overall style cost (J_style)

Once you're done with the loop:

• Return the overall style cost.

def compute_style_cost(model, STYLE_LAYERS):
    """
    Computes the overall style cost from several chosen layers
    
    Arguments:
    model -- our tensorflow model
    STYLE_LAYERS -- A python list containing:
                        - the names of the layers we would like to extract style from
                        - a coefficient for each of them
    
    Returns: 
    J_style -- tensor representing a scalar value, style cost defined above by equation (2)
    """
    
    # initialize the overall style cost
    J_style = 0

    for layer_name, coeff in STYLE_LAYERS:

        # Select the output tensor of the currently selected layer
        out = model[layer_name]

        # Set a_S to be the hidden layer activation from the layer we have selected, by running the session on out
        a_S = sess.run(out)

        # Set a_G to be the hidden layer activation from same layer. Here, a_G references model[layer_name] 
        # and isn't evaluated yet. Later in the code, we'll assign the image G as the model input, so that
        # when we run the session, this will be the activations drawn from the appropriate layer, with G as input.
        a_G = out
        
        # Compute style_cost for the current layer
        J_style_layer = compute_layer_style_cost(a_S, a_G)

        # Add coeff * J_style_layer of this layer to overall style cost
        J_style += coeff * J_style_layer

    return J_style

Note: In the inner-loop of the for-loop above, a_G is a tensor and hasn't been evaluated yet. It will be evaluated and updated at each iteration when we run the TensorFlow graph in model_nn() below.

What you should remember

• The style of an image can be represented using the Gram matrix of a hidden layer's activations.
• We get even better results by combining this representation from multiple different layers.
• This is in contrast to the content representation, where usually using just a single hidden layer is sufficient.
• Minimizing the style cost will cause the image $G$ to follow the style of the image $S$.

3.3 - Defining the total cost to optimize

Finally, let's create a cost function that minimizes both the style and the content cost. The formula is:

$$J(G) = \alpha J_{content}(C,G) + \beta J_{style}(S,G)$$

Exercise: Implement the total cost function which includes both the content cost and the style cost.

# GRADED FUNCTION: total_cost

def total_cost(J_content, J_style, alpha = 10, beta = 40):
    """
    Computes the total cost function
    
    Arguments:
    J_content -- content cost coded above
    J_style -- style cost coded above
    alpha -- hyperparameter weighting the importance of the content cost
    beta -- hyperparameter weighting the importance of the style cost
    
    Returns:
    J -- total cost as defined by the formula above.
    """
    
    ### START CODE HERE ### (≈1 line)
    J = alpha*J_content + beta*J_style
    ### END CODE HERE ###
    
    return J

tf.reset_default_graph()

with tf.Session() as test:
    np.random.seed(3)
    J_content = np.random.randn()    
    J_style = np.random.randn()
    J = total_cost(J_content, J_style)
    print("J = " + str(J))

J = 35.34667875478276

Expected Output:

**J**

35.34667875478276

What you should remember

• The total cost is a linear combination of the content cost $J_{content}(C,G)$ and the style cost $J_{style}(S,G)$.
• $\alpha$ and $\beta$ are hyperparameters that control the relative weighting between content and style.

4 - Solving the optimization problem

Finally, let's put everything together to implement Neural Style Transfer!

Here's what the program will have to do:

1. Create an Interactive Session
2. Load the content image
3. Load the style image
4. Randomly initialize the image to be generated
5. Load the VGG19 model
6. Build the TensorFlow graph:
   • Run the content image through the VGG19 model and compute the content cost
   • Run the style image through the VGG19 model and compute the style cost
   • Compute the total cost
   • Define the optimizer and the learning rate
7. Initialize the TensorFlow graph and run it for a large number of iterations, updating the generated image at every step.

Lets go through the individual steps in detail.

Interactive Sessions

You've previously implemented the overall cost $J(G)$. We'll now set up TensorFlow to optimize this with respect to $G$.

• To do so, your program has to reset the graph and use an "Interactive Session".
• Unlike a regular session, the "Interactive Session" installs itself as the default session to build a graph.
• This allows you to run variables without constantly needing to refer to the session object (calling "sess.run()"), which simplifies the code.

Start the interactive session.

# Reset the graph
tf.reset_default_graph()

# Start interactive session
sess = tf.InteractiveSession()

Content image

Let's load, reshape, and normalize our "content" image (the Louvre museum picture):

content_image = scipy.misc.imread("images/louvre_small.jpg")
content_image = reshape_and_normalize_image(content_image)

Style image

Let's load, reshape and normalize our "style" image (Claude Monet's painting):

style_image = scipy.misc.imread("images/monet.jpg")
style_image = reshape_and_normalize_image(style_image)

Generated image correlated with content image

Now, we initialize the "generated" image as a noisy image created from the content_image.

• The generated image is slightly correlated with the content image.
• By initializing the pixels of the generated image to be mostly noise but slightly correlated with the content image, this will help the content of the "generated" image more rapidly match the content of the "content" image.
• Feel free to look in nst_utils.py to see the details of generate_noise_image(...); to do so, click "File-->Open..." at the upper-left corner of this Jupyter notebook.

generated_image = generate_noise_image(content_image)
imshow(generated_image[0]);

Load pre-trained VGG19 model

Next, as explained in part (2), let's load the VGG19 model.

model = load_vgg_model("pretrained-model/imagenet-vgg-verydeep-19.mat")

Content Cost

To get the program to compute the content cost, we will now assign a_C and a_G to be the appropriate hidden layer activations. We will use layer conv4_2 to compute the content cost. The code below does the following:

1. Assign the content image to be the input to the VGG model.
2. Set a_C to be the tensor giving the hidden layer activation for layer "conv4_2".
3. Set a_G to be the tensor giving the hidden layer activation for the same layer.
4. Compute the content cost using a_C and a_G.

Note: At this point, a_G is a tensor and hasn't been evaluated. It will be evaluated and updated at each iteration when we run the Tensorflow graph in model_nn() below.

# Assign the content image to be the input of the VGG model.  
sess.run(model['input'].assign(content_image))

# Select the output tensor of layer conv4_2
out = model['conv4_2']

# Set a_C to be the hidden layer activation from the layer we have selected
a_C = sess.run(out)

# Set a_G to be the hidden layer activation from same layer. Here, a_G references model['conv4_2'] 
# and isn't evaluated yet. Later in the code, we'll assign the image G as the model input, so that
# when we run the session, this will be the activations drawn from the appropriate layer, with G as input.
a_G = out

# Compute the content cost
J_content = compute_content_cost(a_C, a_G)

Style cost

# Assign the input of the model to be the "style" image 
sess.run(model['input'].assign(style_image))

# Compute the style cost
J_style = compute_style_cost(model, STYLE_LAYERS)

Exercise: total cost

• Now that you have J_content and J_style, compute the total cost J by calling total_cost().
• Use alpha = 10 and beta = 40.

### START CODE HERE ### (1 line)
J = total_cost(J_content, J_style, alpha = 10, beta = 40)
### END CODE HERE ###

Optimizer

• Use the Adam optimizer to minimize the total cost J.
• Use a learning rate of 2.0.
• Adam Optimizer documentation

# define optimizer (1 line)
optimizer = tf.train.AdamOptimizer(2.0)

# define train_step (1 line)
train_step = optimizer.minimize(J)

Exercise: implement the model

• Implement the model_nn() function.
• The function initializes the variables of the tensorflow graph,
• assigns the input image (initial generated image) as the input of the VGG19 model
• and runs the train_step tensor (it was created in the code above this function) for a large number of steps.

Hints

• To initialize global variables, use this:

  sess.run(tf.global_variables_initializer())
  

• Run sess.run() to evaluate a variable.
• assign can be used like this:

  model["input"].assign(image)
  

def model_nn(sess, input_image, num_iterations = 200):
    
    # Initialize global variables (you need to run the session on the initializer)
    ### START CODE HERE ### (1 line)
    sess.run(tf.global_variables_initializer())
    ### END CODE HERE ###
    
    # Run the noisy input image (initial generated image) through the model. Use assign().
    ### START CODE HERE ### (1 line)
    sess.run(model["input"].assign(input_image))
    ### END CODE HERE ###
    
    for i in range(num_iterations):
    
        # Run the session on the train_step to minimize the total cost
        ### START CODE HERE ### (1 line)
        sess.run(train_step)
        ### END CODE HERE ###
        
        # Compute the generated image by running the session on the current model['input']
        ### START CODE HERE ### (1 line)
        generated_image = sess.run(model['input'])
        ### END CODE HERE ###

        # Print every 20 iteration.
        if i%20 == 0:
            Jt, Jc, Js = sess.run([J, J_content, J_style])
            print("Iteration " + str(i) + " :")
            print("total cost = " + str(Jt))
            print("content cost = " + str(Jc))
            print("style cost = " + str(Js))
            
            # save current generated image in the "/output" directory
            save_image("output/" + str(i) + ".png", generated_image)
    
    # save last generated image
    save_image('output/generated_image.jpg', generated_image)
    
    return generated_image

Run the following cell to generate an artistic image. It should take about 3min on CPU for every 20 iterations but you start observing attractive results after ≈140 iterations. Neural Style Transfer is generally trained using GPUs.

model_nn(sess, generated_image)

Iteration 0 :
total cost = 5.05035e+09
content cost = 7877.68
style cost = 1.26257e+08
Iteration 20 :
total cost = 9.43272e+08
content cost = 15187.2
style cost = 2.3578e+07
Iteration 40 :
total cost = 4.84905e+08
content cost = 16785.1
style cost = 1.21184e+07
Iteration 60 :
total cost = 3.12573e+08
content cost = 17466.2
style cost = 7.80995e+06
Iteration 80 :
total cost = 2.28117e+08
content cost = 17715.3
style cost = 5.69849e+06

Expected Output:

**Iteration 0 : **

total cost = 5.05035e+09 content cost = 7877.67 style cost = 1.26257e+08

You're done! After running this, in the upper bar of the notebook click on "File" and then "Open". Go to the "/output" directory to see all the saved images. Open "generated_image" to see the generated image! :)

You should see something the image presented below on the right:

We didn't want you to wait too long to see an initial result, and so had set the hyperparameters accordingly. To get the best looking results, running the optimization algorithm longer (and perhaps with a smaller learning rate) might work better. After completing and submitting this assignment, we encourage you to come back and play more with this notebook, and see if you can generate even better looking images.

Here are few other examples:

• The beautiful ruins of the ancient city of Persepolis (Iran) with the style of Van Gogh (The Starry Night)

• The tomb of Cyrus the great in Pasargadae with the style of a Ceramic Kashi from Ispahan.

• A scientific study of a turbulent fluid with the style of a abstract blue fluid painting.

5 - Test with your own image (Optional/Ungraded)

Finally, you can also rerun the algorithm on your own images!

To do so, go back to part 4 and change the content image and style image with your own pictures. In detail, here's what you should do:

1. Click on "File -> Open" in the upper tab of the notebook
2. Go to "/images" and upload your images (requirement: (WIDTH = 300, HEIGHT = 225)), rename them "my_content.png" and "my_style.png" for example.
3. Change the code in part (3.4) from :

   content_image = scipy.misc.imread("images/louvre.jpg")
   style_image = scipy.misc.imread("images/claude-monet.jpg")
   

   to:

   content_image = scipy.misc.imread("images/my_content.jpg")
   style_image = scipy.misc.imread("images/my_style.jpg")
   

4. Rerun the cells (you may need to restart the Kernel in the upper tab of the notebook).

You can share your generated images with us on social media with the hashtag #deeplearniNgAI or by direct tagging!

You can also tune your hyperparameters:

• Which layers are responsible for representing the style? STYLE_LAYERS
• How many iterations do you want to run the algorithm? num_iterations
• What is the relative weighting between content and style? alpha/beta

6 - Conclusion

Great job on completing this assignment! You are now able to use Neural Style Transfer to generate artistic images. This is also your first time building a model in which the optimization algorithm updates the pixel values rather than the neural network's parameters. Deep learning has many different types of models and this is only one of them!

What you should remember

• Neural Style Transfer is an algorithm that given a content image C and a style image S can generate an artistic image
• It uses representations (hidden layer activations) based on a pretrained ConvNet.
• The content cost function is computed using one hidden layer's activations.
• The style cost function for one layer is computed using the Gram matrix of that layer's activations. The overall style cost function is obtained using several hidden layers.
• Optimizing the total cost function results in synthesizing new images.

Congratulations on finishing the course!

This was the final programming exercise of this course. Congratulations--you've finished all the programming exercises of this course on Convolutional Networks! We hope to also see you in Course 5, on Sequence models!

References:

The Neural Style Transfer algorithm was due to Gatys et al. (2015). Harish Narayanan and Github user "log0" also have highly readable write-ups from which we drew inspiration. The pre-trained network used in this implementation is a VGG network, which is due to Simonyan and Zisserman (2015). Pre-trained weights were from the work of the MathConvNet team.

• Leon A. Gatys, Alexander S. Ecker, Matthias Bethge, (2015). A Neural Algorithm of Artistic Style
• Harish Narayanan, Convolutional neural networks for artistic style transfer.
• Log0, TensorFlow Implementation of "A Neural Algorithm of Artistic Style".
• Karen Simonyan and Andrew Zisserman (2015). Very deep convolutional networks for large-scale image recognition
• MatConvNet.